Fast cosmology with machine learning

One of the most common problems in all areas of science is estimating the parameters of theoretical models using experimental data. For complex models with many parameters this problem can be computationally intensive. Dr Grigor Aslanyan and his colleagues from the Physics department at the University of Auckland have developed a machine learning algorithm that can greatly reduce the computational power required. They tested their algorithm on the standard cosmological model – more commonly known as the Big Bang theory.

“In this work we have developed a machine learning algorithm that can significantly reduce the computational time for parameter estimation”, says Dr Aslanyan. The algorithm was successfully applied to the analysis of the cosmic microwave background (CMB) radiation data from the Planck satellite, yielding results 6.5 times faster when compared with to traditional methods without the application of the algorithm. Dr Aslanyan further notes that their algorithm “is very generic and can be easily applied to a large variety of scientific problems.”

Estimating the parameters

Parameter estimation is typically done by calculating the so-called likelihood function for many different values of the parameters. For each point in the parameter space the likelihood function gives the probability of obtaining the experimental data that was obtained if the theoretical parameters had the given values. “By scanning through the parameter space and calculating the likelihood function for many different values of the parameters, one can learn which parameter values are more likely, from which an estimated range of the parameters can be obtained”, explains Dr Aslanyan. For example, the standard cosmological model is described by six parameters, which include the amount of dark matter and dark energy in the Universe as well as its expansion rate. Using the CMB radiation data, a likelihood function is constructed, which can tell which values of these parameters are more likely. “By probing many different values, we are able to determine the values of the parameters and their uncertainties from the data.”

Many different statistical methods have been developed for parameter estimation, including Markov Chain Monte Carlo (MCMC) sampling and nested sampling. The choice of which method to use depends strongly on the specific problem. However, although there are significant differences between different methods, all of the methods have one thing in common – they all require the calculation of the likelihood function many times for different parameter values. “For problems with a large number of parameters, as well as problems with slow likelihood functions, the parameter estimation can become computationally expensive”, says Dr Aslanyan. ”Our work aims to reduce the computational time for the calculations of these slow likelihood functions.”

A Machine Learning Algorithm

The machine learning algorithm developed by Dr Aslanyan uses the results of likelihood calculation to train itself, and after some training period is able to accurately approximate the likelihood function very rapidly for certain points in the parameter space, instead of doing the slow likelihood calculation. “What distinguishes our algorithm from previously developed similar tools is its ability to estimate and control the error it makes. Also, it does not require an initial training period, although providing a training set can result in a better speed-up. The algorithm has no dependence on the statistical method of sampling, so it can be used with any sampling method.”

Attribution: 

Figure 1.

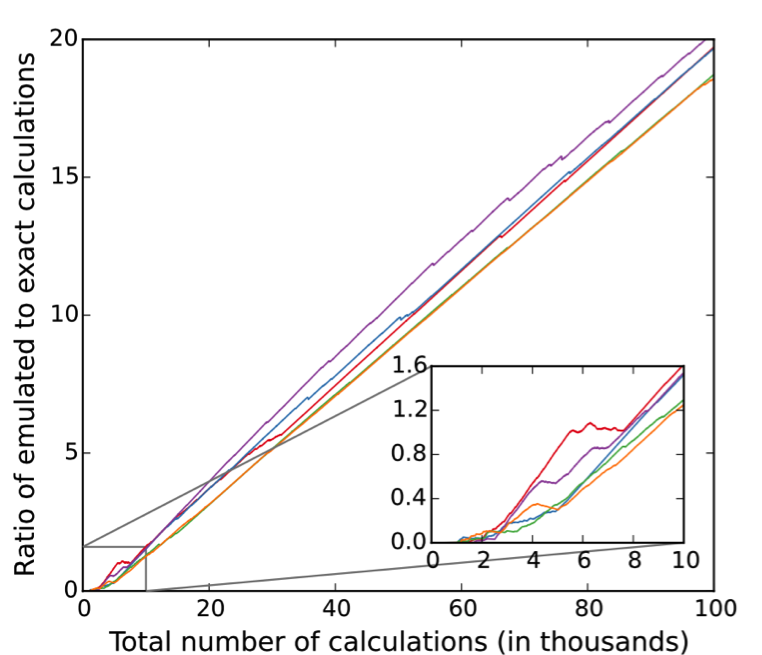
The figure above demonstrates the efficiency of the algorithm for cosmological parameter estimation. The horizontal axis shows the total number of likelihood calculations, and the vertical axis shows the ratio of the number of emulated calculations (fast) to the number of exact calculations (slow). The algorithm was run in parallel on multiple nodes, and the different colors in the plot show the results for different nodes. As can be seen in the plot, at the beginning of the run the ratio of emulated to exact calculations is 0 and grows slowly, since the algorithm needs some exact calculations to train itself. However, shortly after starting the scan, the ratio starts increasing, reaching about 20 by the end of the run. This means that the algorithm was able to eliminate about 95% of the required slow likelihood calculations, replacing them with very fast and accurate approximations. This resulted in an overall factor of 6.5 speedup, finishing the run in a few hours instead of about two days.

“The use of the NeSI computational resources was crucial for completing this project”, explains Dr Aslanyan. “Since the main aim of our algorithm is to reduce the computational time of computationally very intensive problems, we would not be able to do any runs on a desktop. The cosmological example that we worked on typically requires a few days on about 50 CPU cores. We had to do many runs for many examples to be able to configure the details of our algorithm. Moreover, our algorithm is designed to take advantage of parallelism. Running the algorithm on many parallel nodes would have been impossible without the NeSI cluster.”

Dr Aslanyan’s work was published in JCAP 09 (2015) 005. The paper is also available on arXiv, 1506.01079. The algorithm has been implemented in C++ and is publicly available as a part of the Cosmo++ package at http://cosmo.grigoraslanyan.com.